Courrier des statistiques N10 - 2023
Peut-on se fier aux sondages empiriques ?
Les enquêtes par sondage s’appuient sur un échantillon probabiliste ou sur un échantillon empirique. Dans l’approche empirique, la probabilité d’être enquêté, pour un individu donné, est généralement dépendante de la valeur de la variable que l’on collecte auprès de cet individu. Cela produit une erreur particulière appelée ‘biais de sélection’. Dans la méthode empirique dite « des quotas », on limite ce biais en structurant l’échantillon selon certaines variables expliquant le phénomène mesuré. Néanmoins, un biais subsiste si ces variables ne suffisent pas à en appréhender toute la variabilité. Pour justifier pleinement la méthode, on fait appel à une hypothèse de comportement des individus, appelée modélisation. D’autres méthodes de sélection empiriques existent, comme la méthode des unités‑type − traduisant la perception que l’on a communément de la « représentativité » − ou l’échantillonnage de volontaires, particulièrement développé ces dernières années au travers des « Access panels ». Dans ce dernier cas, le biais de sélection peut être important, voire considérable. Malheureusement, on ne réduit pas le biais en augmentant la taille de l’échantillon. Deux exemples spectaculaires − l’un portant sur le taux de couverture vaccinale contre le coronavirus, l’autre sur les élections présidentielles de 1936 aux États‑Unis − illustrent ce phénomène, dit « paradoxe des big data ».
- Sondage probabiliste et sondage empirique : un schisme méthodologique
- Les enquêtes par quotas, méthodologie standard du sondage empirique
- Face aux échantillonnages probabilistes, un double handicap quant à la qualité
- Les erreurs dans les enquêtes par sondage
- Le problème spécifique du biais dans les enquêtes empiriques
- La meilleure façon de justifier statistiquement les enquêtes par quotas
- Encadré 1. La justification par modèle de la méthode des quotas
- Échantillonnage probabiliste ou échantillonnage par quotas ?
- Encadré 2. Comparaison des sondages probabiliste et empirique en matière d’erreur d’échantillonnage
- D’autres techniques d’échantillonnage empirique : unités-type, échantillons de volontaires, et « Access panels »
- Le paradoxe des big data : un exemple catastrophique récent...
- ... un précédent tout aussi révélateur
- En guise de conclusion
- Annexe. L’origine du biais dans les sondages empiriques
Le statisticien est par nature confronté à des problèmes d’estimation. Il cherche en effet à approcher au plus près différentes « grandeurs » dont personne ne connaît a priori la valeur exacte. Ces grandeurs, qualifiées de « paramètres d’intérêt », sont définies dans une population (individus, entreprises, articles de vente, etc.) généralement de très grande taille, à partir de variables individuelles quantitatives ou qualitatives que l’on appelle « variables d’intérêt ». La plupart des paramètres sont des moyennes ou se construisent à partir de moyennes (totaux, proportions, dispersions). Par exemple, on s’intéresse au revenu moyen des personnes résidant en Bretagne à une date donnée, au chiffre d’affaires total annuel des boulangeries parisiennes, ou encore à l’évolution des prix moyens de l’alimentaire entre deux mois consécutifs. Dans ce contexte, la statistique la plus précise relève d’une collecte exhaustive, donc d’un recensement. Le coût d’un recensement étant généralement dissuasif, on utilise, en pratique, des techniques de sondage consistant à restreindre la collecte à une sous-population, l’échantillon. Les techniques d’échantillonnage distinguent deux grandes familles : les sondages probabilistes et les sondages empiriques (Ardilly & Lavallée, 2017). Ces derniers s’appuient parfois sur des échantillons de volontaires – les fameux « Access panels » – et utilisent très souvent la célèbre méthode de sondage « par quotas ». Ils séduisent du fait de la rapidité de la mise en œuvre et de l’économie de moyens, tandis que le respect des quotas a un côté rassurant. Certes, utiliser un sondage est toujours une prise de risque, mais avec ces méthodes, une prudence toute particulière est requise. Pourquoi, et que peut-on leur reprocher ?
Dans cet article, on cherche à répondre à cette question en insistant sur les erreurs que produisent le plus souvent les échantillonnages empiriques. En particulier, on ne peut pas les réduire en se contentant d’augmenter la taille de l’échantillon. En revanche, elles peuvent disparaître si on accepte certaines hypothèses portant sur les variables d’intérêt considérées. Un changement de paradigme permet de construire un cadre théorique généralement utilisé pour l’expliquer.
Sondage probabiliste et sondage empirique : un schisme méthodologique
Dans la réalisation d’une enquête par sondage, le statisticien distingue quatre étapes : l’échantillonnage, la collecte, l’estimation, et le calcul de précision. L’échantillonnage – sauf cas très particulier des unités-type (cf. infra) − constitue une source majeure d’aléa : il s’agit de désigner les unités auprès desquelles on va collecter l’information. L’étape suivante est celle de la collecte, qui doit respecter de nombreuses consignes et qui produit presque toujours de la non-réponse. La non-réponse introduit une seconde source d’aléa, qu’il est souhaitable de minimiser. Vient ensuite l’estimation, étape calculatoire qui agrège de façon adéquate les données individuelles collectées afin d’estimer le paramètre d’intérêt. L’opération s’achève par la mesure d’erreur, communément appelée « calcul de précision ».
Dans une population donnée, la sélection d’un échantillon quelconque peut être aléatoire ou non, et si elle est aléatoire, on peut être capable ou non de calculer la probabilité d’obtenir l’échantillon en question. Le contexte dans lequel l’échantillonnage permet une maîtrise des probabilités de sélection est celui de l’échantillonnage probabiliste. Par « maîtrise », il faut comprendre que la méthode d’échantillonnage mise en œuvre autorise un calcul théorique de ces probabilités. Dans le cas contraire, on a affaire à un échantillonnage empirique.
Les fondements de l’échantillonnage probabiliste attribuent un rôle central à la base de sondage et à l’algorithme de sélection. La base de sondage est la liste exhaustive et sans double compte des individus formant la population d’intérêt. Sur cette base, on applique un algorithme, c’est-à-dire une règle objective (sans intervention humaine) et entièrement codifiée, de sélection aléatoire des individus de l’échantillon. Dans ces conditions, on peut connaître, pour chaque individu de la base de sondage, la probabilité qu’il appartienne à l’échantillon. On en déduit un poids de sondage, facteur déterminant qui traduit le nombre d’unités de la population que l’individu échantillonné représente. On multiplie le poids de sondage de chaque individu par ses réponses au questionnaire, et la résultante est sommée sur l’échantillon pour produire les estimations attendues. En pratique, on est confronté à la non-réponse, que l’on traite généralement en corrigeant les poids. L’ampleur numérique de cette correction est importante : elle consiste, dans l’approche la plus fruste, à multiplier les poids par l’inverse de la proportion de répondants dans l’échantillon tiré. On ajoute presque toujours une étape finale dite de redressement (ou de calage) qui consiste à modifier de nouveau les poids – de manière marginale cette fois – pour améliorer la qualité de l’estimation (Ardilly, 2006 ; Lohr, 2021).
À l’inverse, l’échantillonnage empirique, lorsqu’il est aléatoire, relève d’une pratique de sélection qui ne permet pas le calcul de la probabilité de sélection des échantillons ni celle des individus de la population. Non pas qu’il s’agisse d’une impuissance mathématique des statisticiens, mais parce que cette sélection résulte par nature d’un processus en partie subjectif. En pratique, on confie ce rôle à des enquêteurs ou on s’en remet au volontariat des participants, perdant ainsi la maîtrise des probabilités de tirage : on peut parfaitement imposer et superviser la façon dont fonctionne un programme informatique de sélection, mais ce contrôle n’est plus possible lorsque la sélection résulte en partie du comportement humain !
Les enquêtes par quotas, méthodologie standard du sondage empirique
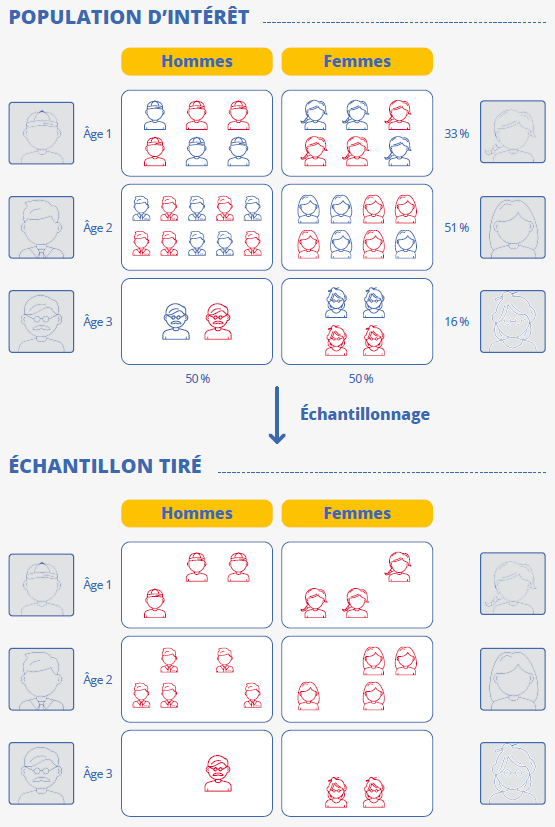
La sélection empirique la plus commune est faite « sur le terrain » par des enquêteurs, en face à face ou par téléphone, en s’appuyant sur un ensemble de consignes qui tendent à reproduire autant que possible un mécanisme probabiliste uniforme où tous les individus ont exactement la même chance d’être tirés. L’objectif consiste à rendre cette sélection aléatoire autant que possible, en évitant de privilégier certaines catégories de population. Une façon naturelle de réduire ce risque passe par le respect de quotas – d’où le nom de « méthodes par quotas ». Il s’agit de définir des sous-populations à partir des modalités d’un jeu de variables qualitatives ou quantitatives (les « variables de quotas ») découpées en tranches, et de demander à chaque enquêteur de constituer un échantillon dont les effectifs appartenant à ces différentes sous-populations – les quotas – soient égaux à ce que produirait « en moyenne » un échantillonnage probabiliste à probabilités égales (dit « équiprobable »). Par exemple, on demande à ce que l’échantillon empirique comprenne moitié d’hommes et moitié de femmes, parce qu’il s’agit de la structure par sexe « moyenne » résultant d’un échantillonnage aléatoire équiprobable. C’est aussi la vraie structure de la population française selon cette variable. On évitera ainsi qu’un enquêteur ne produise un échantillon trop déséquilibré sur la variable sexe, ce qui éloignerait le processus de sélection d’un processus équiprobable. La plupart du temps, on impose un jeu de quotas construits en croisant plusieurs variables – par exemple simultanément le sexe, l’age et le diplôme (figure 1). Ainsi, on dispose au final d’un échantillon qui a les caractéristiques d’une photo-réduction de la population d’intérêt en ce qui concerne les variables de quotas. La méthode permet de se passer d’une base de sondage : c’est un avantage considérable, car les bases sont souvent coûteuses à acquérir et elles peuvent être couvertes en amont par la confidentialité des données individuelles.
Figure 1 - Échantillonnage par quotas
Face aux échantillonnages probabilistes, un double handicap quant à la qualité
Le respect des quotas est une condition nécessaire mais non suffisante pour qu’on puisse assimiler l’échantillonnage empirique à du tirage aléatoire équiprobable. Pour apprécier la nature du risque, imaginons une enquête sur l’emploi du temps et imposons des quotas construits à partir du sexe et de l’âge. L’échantillon final respectera donc la structure de la population d’intérêt selon ces deux critères. Les enquêteurs, sur le terrain, en mode face-à- face ou en mode téléphone, vont sélectionner des individus consentants, et a priori ils vont le faire durant la journée, aux horaires durant lesquels la plupart des actifs exercent leur profession. Ainsi, il est fort probable que l’échantillon soit déficitaire en certaines catégories d’actifs, ceux que l’on peut contacter tôt le matin, tard le soir, voire parfois seulement la nuit. À l’inverse, on « surcharge » l’échantillon en personnes sans emploi, plus faciles à contacter en journée. Évidemment, dans le cas présent, la ficelle est assez grosse, et on limitera ce risque en agissant ici dans trois directions au moins : on enrichira les quotas en ajoutant au moins une variable liée à l’activité, on demandera aux enquêteurs d’élargir leurs horaires de collecte en semaine et de travailler le week-end, et on étendra la période de collecte. On enrichira les quotas... à condition qu’on puisse déterminer les variables en rapport suffisamment étroit avec l’emploi du temps, à condition qu’on connaisse la structure de la population selon les modalités de ces variables, à condition aussi que les contraintes générées par l’accumulation des quotas ne rendent pas la collecte insupportable pour les enquêteurs. Par ailleurs, on ne pourra probablement élargir les horaires de collecte que jusqu’à un certain point. Ainsi, même si on parvient à réduire sensiblement les risques, il n’y aura aucune garantie qu’il ne reste pas une ou plusieurs variables cachées explicatives de l’emploi du temps mais gérées (en toute inconscience) de manière déséquilibrée par le réseau d’enquêteurs. A contrario, l’échantillonnage probabiliste à probabilités égales dispose d’un avantage fort en éliminant ce type de risque, car il produit un échantillon équilibré « en moyenne » sur n’importe quelle variable.
Dans la pratique, le phénomène de non-réponse joue comme une phase d’échantillonnage supplémentaire – non-contrôlée par le statisticien − qui vient réduire la qualité des estimations. Les deux types d’échantillonnage sont affectés par la non-réponse mais la collecte qui suit l’échantillonnage probabiliste impose une multiplication des tentatives de contact auprès de chaque individu échantillonné impossible à joindre, cela jusqu’à atteindre un seuil de renoncement. En revanche, dans un sondage empirique, un individu échantillonné mais non-répondant est définitivement ignoré si sa variable d’intérêt n’est pas immédiatement collectée. L’approche empirique prend un avantage très substantiel en termes de coût, mais à l’issue de la collecte, la non-réponse a sensiblement moins déséquilibré un échantillon probabiliste qu’elle ne le fait avec un échantillon empirique.
Ce phénomène insidieux est souvent ignoré parce que la non-réponse est occultée dans les approches empiriques : non quantifiée, il n’en est à peu près jamais fait état et elle semble même inexistante pour les utilisateurs des données puisque l’échantillon final a toujours par construction la taille initialement requise. Sur ce point, l’échantillonnage probabiliste offre un avantage comparatif parce qu’il est possible d’estimer par modèle les probabilités de réponse et d’apporter des corrections qui limitent l’effet négatif de la non-réponse ; néanmoins, les imperfections (inévitables) de cette phase corrective produisent in fine un biais d’estimation.
Les erreurs dans les enquêtes par sondage
Différents types d’erreur affectent les enquêtes par sondage (Blog Insee, 2022). On peut en distinguer quatre.
La première erreur est celle du défaut de couverture, qui survient lorsque certains individus de la population d’intérêt ne peuvent pas être échantillonnés. Dans les enquêtes probabilistes, c’est dû à un éventuel défaut d’exhaustivité de la base de sondage. Dans les enquêtes empiriques, en l’absence de base de sondage, ce type d’erreur est plus difficile à cerner, mais on en imagine facilement les manifestations. En particulier, pour une collecte en face à face auprès de personnes physiques, il est fort probable que certains individus soient consciemment rejetés par l’enquêteur – parce qu’ils sont par exemple d’accès difficile ou simplement dissuadent a priori l’enquêteur de par leur apparence ou leur comportement peu engageant. En effet, lorsqu’on a le choix de l’enquêté, on a naturellement tendance à se porter vers des individus qui semblent « faciles » à aborder.
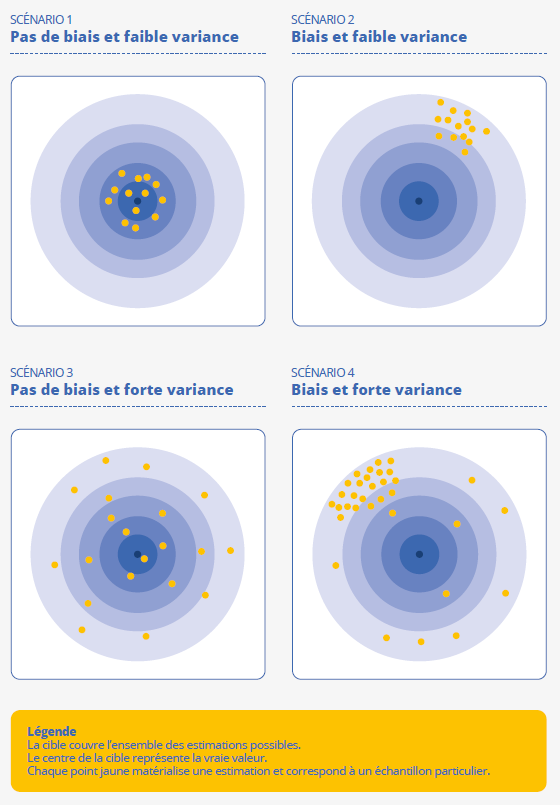
La seconde erreur est l’erreur d’échantillonnage. Cette erreur traduit le fait que les estimations produites sont sensibles à la composition de l’échantillon et qu’elles ne sauraient donc coïncider avec la valeur « exacte » du paramètre d’intérêt. Deux composantes sont identifiables : le biais et la variance (figure 2).
Figure 2 - Biais et variance
Supposons que l’on tire un grand nombre d’échantillons, selon une méthode donnée,
et que chaque échantillon produise son estimation. Si la moyenne de toutes les estimations
obtenues à partir de tous ces échantillons diffère de la vraie valeur, on dit qu’il
y a un biais d’estimation. Cela peut provenir par exemple de déséquilibres systématiques
dans la composition de l’échantillon. Par ailleurs, l’hétérogénéité des différentes
estimations peut être formalisée au travers d’un indicateur appelé variance d’échantillonnage :
plus il y a de dispersion des estimations, plus la variance est grande, et moins la
qualité d’estimation sera bonne. Une grande variance signifie donc que l’estimation
dépend fortement de l’échantillon, ce qui n’est évidemment pas souhaitable. De façon
générale, la variance d’une estimation dépend de trois facteurs : le système de pondération
utilisé − qui essentiellement reflète la méthode d’échantillonnage adoptée − la taille
de l’échantillon tiré, et l’ampleur de la non-réponse. Quelle que soit la méthode
d’échantillonnage, la variance diminue lorsque la taille de l’échantillon répondant
augmente.
La troisième erreur, déjà abordée, est due à la non-réponse, qui provient essentiellement de problèmes de localisation (dans les enquêtes probabilistes en face-à-face), de comportements de refus de l’enquêté et d’impossibilité à joindre l’enquêté (dans les enquêtes par téléphone par exemple).
Pour terminer, citons l’erreur d’observation, qui survient chaque fois que l’information collectée n’est pas conforme à la réalité (par exemple à la suite d’une mauvaise déclaration de l’enquêté – consciemment ou non − ou d’erreur de saisie de l’enquêteur, voire d’une mauvaise formulation des questions). Sur ce type d’erreur, il n’y a pas lieu de penser que la nature de l’échantillonnage ait un effet particulier. L’erreur d’observation est distinguable des précédentes en ce sens où elle traduit une véritable « faute » humaine : les autres erreurs sont plutôt de la nature d’imperfections dont la responsabilité revient au contexte, ou tout simplement au hasard.
Le problème spécifique du biais dans les enquêtes empiriques
On critique parfois la méthode des quotas parce qu’elle produit des estimations biaisées. L’origine fondamentale de ce biais est l’impossibilité de construire un système de pondération qui corresponde à l’échantillonnage pratiqué et à la non-réponse (on rappelle ici que la formulation du poids dépend théoriquement de la probabilité de sélection). De fait, puisqu’on ne maîtrise pas les probabilités de sélection et que l’on ne sait rien de la non-réponse, les estimations issues des échantillonnages empiriques sont toujours construites à partir de poids constants. Ainsi, pour estimer des moyennes dans la population d’intérêt, on calcule des moyennes simples dans l’échantillon : c’est faute de pouvoir faire autrement, et c’est là le point faible majeur des enquêtes par quotas ! Formellement, on peut montrer (annexe) que l’ampleur du biais est conditionnée par la corrélation existante entre la variable d’intérêt et la probabilité de sélection des individus de la population. C’est assez intuitif : si on reprend l’exemple de l’enquête Emploi du temps, on peut craindre que la probabilité d’enquêter un individu soit plus forte si cet individu travaille moins. Un échantillonnage probabiliste n’aura pas ce défaut, parce que le processus de sélection ne sera en rien influencé par la nature de l’activité de l’enquêté – ou si tel est le cas, ce sera d’une manière parfaitement contrôlée. Néanmoins, dans une enquête probabiliste la non-réponse génère a priori un biais ; il est donc important de chercher à avoir le taux de réponse le plus élevé possible.
Annuler la corrélation entre deux variables qui n’ont aucune raison de ne pas être corrélées de manière « naturelle » revient à créer les conditions pour rendre constante l’une des deux variables en question. La première façon d’y parvenir est d’agir afin que la probabilité de sélection soit constante. C’est précisément ce que l’échantillonnage empirique ne parvient pas à faire de manière rigoureuse en pratique, mais on cherche naturellement à se rapprocher de cette situation idéale − qui est évidemment celle de l’échantillonnage aléatoire équiprobable. C’est pourquoi il est absolument essentiel de donner des instructions aux enquêteurs pour rendre ce processus aléatoire au maximum, afin que la collecte soit la moins sélective possible. Ce sont en pratique des instructions de bon sens, consistant à parcourir des zones variées, ne pas interroger son voisinage exclusivement, varier les horaires de contact ainsi que les jours de collecte... La seconde façon d’annuler la corrélation, c’est de faire en sorte que la variable d’intérêt soit constante. Cette piste semble absurde de prime abord, mais c’est néanmoins celle qui produit la meilleure justification de la méthode des quotas : sa philosophie est portée par l’approche par modèle, exposée ci-après.
La meilleure façon de justifier statistiquement les enquêtes par quotas
La spécificité des enquêtes par sondage tient à la nature de l’aléa du sondage. Dans son approche historique, qui est aussi l’approche par défaut adoptée de nos jours, c’est en effet la composition de l’échantillon qui est aléatoire, et non les variables d’intérêt. On considère ainsi que les données collectées sont déterministes, c’est-à-dire fixées, connues et fournies par l’enquêté (sauf en cas d’erreur d’observation). Et dans ce cas, l’estimation est entachée de biais et de variance. En parallèle, la théorie statistique a développé une autre approche – dite stochastique − qui traite les données collectées auprès d’un individu donné comme la résultante d’un phénomène aléatoire, exactement comme si une loterie avait décidé de leurs valeurs. C’est une autre façon d’aborder la question de l’estimation de paramètres, qui offre un cadre théorique confortable pour justifier l’approche par quotas. L’idée sous-jacente consiste à relier la valeur de la variable d’intérêt aux modalités des variables de quotas, la première étant une fonction simple des secondes, en la circonstance une somme de valeurs caractérisant chaque modalité. Par exemple, on postulera que le temps passé aux tâches domestiques est une fonction du sexe (homme / femme), de l’âge (enfant / âge actif / personne âgée) et du statut d’activité (actif occupé / autre), en retenant ces trois variables et leurs modalités comme variables de quotas pour constituer l’échantillon. Ainsi, en connaissant le sexe, la tranche d’âge et le statut d’activité, on est « presque » en mesure de déterminer le temps passé aux tâches domestiques. Dans ces conditions, il est assez intuitif que seules ces variables sont importantes pour déterminer la composition de l’échantillon : puisque les autres critères ne comptent pas, ou très peu, un éventuel déséquilibre sur ces derniers n’aura pas de conséquence sur l’estimation. En la circonstance, il faut certes que les proportions de femmes, d’enfants, de personnes âgées, et d’actifs occupés au sein de l’échantillon soient celles de la population, mais pour le reste peu importe : si l’échantillon est constitué par ailleurs essentiellement de ruraux peu diplômés et célibataires, y compris de manière grossièrement excessive, il ne faudra pas s’en émouvoir puisque ni le type de commune, ni le diplôme, ni l’état matrimonial ne sont des critères qui influent sur le temps passé aux tâches domestiques.
Un tel état d’esprit fait donc entière confiance à une relation entre variables, ce qui constitue une hypothèse simplificatrice de la réalité : exactement ce qu’on dénomme un « modèle » en statistique.
Les modèles stochastiques proposent par ailleurs un cadre très pratique pour calculer des erreurs (Ouvrir dans un nouvel ongletDeville, 1991). Il ne s’agit plus d’erreurs d’échantillonnage mais d’erreurs d’une autre nature puisque l’aléa est celui qui affecte les valeurs des variables d’intérêt. On part toujours du principe que le modèle est juste en ce sens où la valeur de la variable d’intérêt est en moyenne égale à la somme des valeurs caractérisant les modalités des variables de quotas (encadré 1). Il s’ensuit un principe fondamental : la façon de sélectionner l’échantillon – dès lors qu’il respecte les contraintes de quotas − n’a pas d’importance, et comme corollaire direct, il apparaît dans l’approche stochastique qu’on n’a pas besoin de pondérer les individus échantillonnés (Ouvrir dans un nouvel ongletSmith, 1983). L’utilisation d’une moyenne simple pour estimer une vraie moyenne inconnue trouve donc là sa pleine justification.
On remarque que le modèle standard des quotas consiste à considérer comme constante la variable d’intérêt – à de petits écarts aléatoires près – au sein de chaque sous-population définie par le croisement des modalités des variables de quotas. Il s’agit d’une hypothèse fortement contraignante, d’autant que les variables de quotas sont généralement en nombre limité et que la forme de leur relation avec la variable d’intérêt doit être spécifique (en l’occurrence additive).
Mais ce cadre crée de facto des corrélations (à peu près) nulles entre probabilité de sélection et variable d’intérêt soit, comme signalé précédemment, les conditions d’un biais d’échantillonnage (très) faible − ainsi la boucle est bouclée !
Puisqu’un modèle est la formalisation d’une hypothèse, le risque est évidemment celui d’une hypothèse fausse, qui aurait pour sanction immédiate un biais d’estimation au sens de l’aléa du modèle.
Échantillonnage probabiliste ou échantillonnage par quotas ?
C’est évidemment une question opérationnelle centrale. Lorsqu’on ne dispose pas de base de sondage, nécessité fait loi, car il n’est pas possible de procéder à un échantillonnage probabiliste. C’est une situation assez fréquente, parce que les bases de sondage sont très souvent des fichiers confidentiels constitués et détenus par des organismes publics, qu’il n’est pas possible de diffuser. Pour les personnes physiques, c’est par exemple le cas du Recensement de la population, ou des fichiers fiscaux. Pour les entreprises en revanche, le répertoire Sirene est accessible à tout utilisateur. Il faut ensuite tenir compte des budgets d’enquête : l’enquête probabiliste est sensiblement plus coûteuse puisqu’elle impose des unités échantillonnées. Cela nécessite davantage de tentatives de contact, et des coûts de déplacement plus élevés si le mode de collecte est le face-à-face.
Au-delà de ces éléments logistiques et budgétaires, les considérations de qualité statistique contribuent à la prise de décision (Ouvrir dans un nouvel ongletMac Innis, 2018 ; Ouvrir dans un nouvel ongletBrüggen, 2016 ; Ouvrir dans un nouvel ongletShirani‑Mehr, 2018 ; Forster, 2001). Par construction, et c’est un atout des méthodes de quotas, le respect des quotas restreint la diversité des échantillons et cela se traduit par une réduction de la variance d’échantillonnage. En revanche, cette fois au désavantage des méthodes de quotas, le biais est un facteur pénalisant que n’a pas l’échantillonnage probabiliste si on fait abstraction de la non-réponse (et des défauts de couverture), et on peut vérifier, hélas, que le biais empirique ne se réduit pas quand la taille de l’échantillon augmente. On se trouve conduit à un arbitrage entre biais et variance. Si on s’intéresse à l’erreur d’échantillonnage totale, en tenant compte à la fois du biais et de la variance, il apparaît que les échantillonnages empiriques ne sont pas recommandés pour les gros échantillons. En revanche, les petits échantillons empiriques peuvent être préférables à un échantillon aléatoire équiprobable parce que l’avantage en termes de variance dépasse le handicap du biais (encadré 2). Ce principe est conforme à ce qu’on constate en pratique : les échantillons empiriques dépassent rarement 2 000 unités, et leurs tailles se situent même assez souvent aux alentours de 1 000, voire moins.
Encadré 2. Comparaison des sondages probabiliste et empirique en matière d’erreur d’échantillonnage
Considérant le seul critère de précision statistique, les deux types de sondage ici considérés ont des comportements différents, en particulier au regard de l’effet de la taille de l’échantillon. En voici les principales caractéristiques.
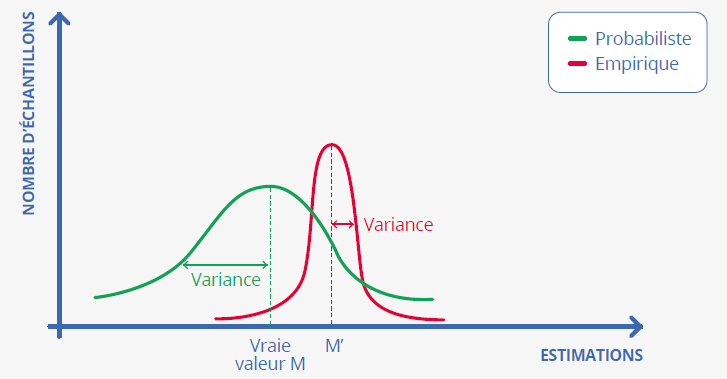
La figure 1 compare la distribution des estimations issues respectivement d ’un échantillonnage
empirique (courbe rouge) et d’un échantillonnage probabiliste simple et équiprobable
(courbe verte), pour une taille d’échantillon donnée et plutôt petite – par exemple
quelques centaines d’unités. Ces courbes ont des allures de courbe de Gauss (« courbe
en cloche »). La courbe probabiliste est centrée sur la vraie valeur M (absence de biais) et elle est plus étalée que la courbe rouge, ce qui traduit une
variance d’échantillonnage plus grande. La courbe rouge est centrée autour d’une valeur
M’ différente de la vraie valeur M, si bien que le biais vaut M’−M.
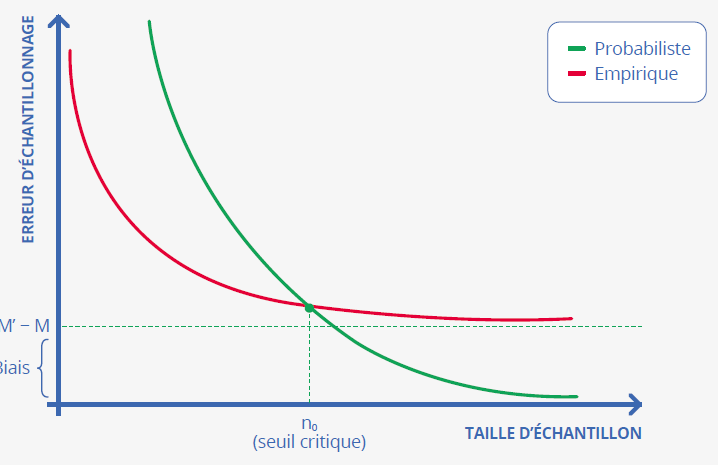
La figure 2 explique comment l’erreur d’échantillonnage, mêlant biais et variance, évolue en fonction de la taille de l’échantillon. Dans le cas probabiliste (courbe verte), l’erreur est grande dans la zone des (très) petites tailles d’échantillon et la variance y contribue beaucoup. Le biais étant toujours nul et la variance tendant vers zéro quand la taille de l’échantillon augmente, la courbe verte décroît jusqu’à (presque) se confondre avec l’axe des abscisses. La courbe rouge se situe en dessous de la verte dans la zone des (très) petites tailles d’échantillon, car le tirage empirique a l’avantage par rapport au tirage probabiliste aléatoire simple et équiprobable (celui qui attribue la même probabilité de tirage à tous les échantillons de taille donnée). Comme le biais est non nul dans le cas empirique, et qu’il n’est pas (ou peu) sensible à la taille d’échantillon, la courbe rouge est décroissante mais tend vers une droite située au-dessus de l’axe de abscisses – positionnée à l’ordonnée M’−M, valeur du biais d’échantillonnage. Les deux courbes se croisent nécessairement « quelque part » et ce croisement définit une taille d’échantillon critique au-dessus de laquelle le sondage empirique est moins efficace que le sondage probabiliste le plus simple qui soit.
D’autres techniques d’échantillonnage empirique : unités-type, échantillons de volontaires, et « Access panels »
Les techniques empiriques d’échantillonnage s’étendent bien au-delà des enquêtes par quotas, qui n’en sont qu’une modalité. Présentons maintenant trois pratiques concurrentielles, la première (les unités-type) étant désormais peu utilisée, alors que la troisième (les « Access panels ») est en plein essor.
Échantillonnage ne veut pas nécessairement dire sélection aléatoire. Historiquement, ce n’est d’ailleurs pas la sélection aléatoire qui a été utilisée dans les premiers temps des enquêtes par sondage, mais plutôt des techniques où on choisissait consciencieusement − et dans l’idéal judicieusement − les individus enquêtés. On peut utiliser le terme très évocateur de « choix raisonné » pour désigner les échantillons définis sans aucune intervention du hasard. C’est une approche qui est entièrement dépendante d’un modèle et qui est donc scientifiquement déviante pour un statisticien qui s’obstine à vouloir éviter les modèles, car il y a nécessairement un biais d’échantillonnage et la variance d’échantillonnage perd son sens. Les individus enquêtés sont ceux qui représentent le mieux, pense-t-on, la population complète, et on peut ainsi parler d’unités-type, ou encore d’individus « représentatifs » de la population. Dans l’exemple de l’enquête sur les tâches domestiques, on pourrait ainsi choisir quelques individus coopératifs dans chaque croisement de modalités des trois variables explicatives retenues. Encore une fois, puisque sous couvert du modèle la méthode de sélection n’a pas d’importance, l’intervention du hasard n’apporte rien. Cette méthode, qui n’est utilisée que dans de rares circonstances bien adaptées, conserve tout son intérêt pour de tous petits échantillons, pour lesquels la variance serait énorme si on laissait au hasard le soin de décider de leur composition. Typiquement, on peut procéder ainsi pour définir un échantillon de quelques départements dans lesquels on effectue ensuite des tirages d’individus. Cette approche est également appliquée par l’Insee dans la sélection de certains produits et points de vente suivis dans l’indice des prix à la consommation.
L’échantillonnage de volontaires renvoie à toutes les situations pour lesquelles on laisse le soin à une partie de la population de participer à une enquête à son entière initiative. Bien sûr, les enquêtes en France sont avant tout placées sous le sceau du volontariat – même si la plupart des enquêtes de la statistique publique sont légalement obligatoires – en ce sens où un refus n’a pratiquement jamais de conséquence significativement pénalisante pour les personnes physiques comme pour les entreprises. Mais les échantillonnages probabilistes, et les échantillonnages empiriques par quotas dans une moindre mesure, sont constitués selon certaines règles qui cherchent en amont à structurer l’échantillon d’une façon efficace et la collecte s’appuie sur des principes qui tendent à préserver au maximum la composition de l’échantillon tiré. Exempt de tout cadrage, l’échantillonnage de volontaires n’a aucune de ces vertus et s’avère de fait scientifiquement critiquable. On trouve essentiellement dans cette catégorie les enquêtes d’opinion sur internet appelant les consommateurs à se prononcer sur un produit ou une prestation. Les indices de satisfaction qui en résultent sont soumis à des risques de biais considérables puisqu’on se trouve dans le cas a priori d’une très forte corrélation entre la probabilité de participation et la variable d’intérêt : il est par exemple assez naturel, pour un consommateur qui est mécontent d’un repas dans un restaurant, de mettre une mauvaise appréciation sur internet, et à l’inverse d’en formuler une très bonne s’il est très satisfait. Mais confronté à une prestation plus standard, fera-t-il cet effort ?
Les échantillons tirés d’« Access panels » relèvent d’un cas intermédiaire enchaînant un échantillonnage de volontaires et un échantillonnage par quotas. Ce vocable désigne un ensemble de pratiques probablement assez diversifiées, mais dans bon nombre de cas il s’agit de constituer en amont un échantillon de volontaires de très grande taille, géré en continu, servant de base de sondage pour produire ensuite au fil de l’eau des échantillons beaucoup plus petits respectant des quotas de circonstance – avec les risques que l’on vient d’exposer en termes de biais. Il ne faut pas négliger le fait que les volontaires reçoivent des gratifications, sous différentes formes, en contrepartie de leur participation, et cela n’est très probablement pas sans conséquence sur la composition des échantillons, quoi qu’on en dise. Un « Access panel » a l’avantage de produire à moindre coût des échantillons d’individus présentant un profil ciblé, allant jusqu’à permettre de sonder des populations rares, mais c’est une source de données à géométrie variable qui peut se révéler d’une grande opacité pour les utilisateurs. De telles situations doivent éveiller la méfiance : le manque d’informations sur les méthodes est de façon générale problématique, et dans ce cas précis pose question si le processus de constitution et de gestion de l’« Access panel », ainsi que sa structure, ne sont pas explicites.
Le paradoxe des big data : un exemple catastrophique récent...
On a coutume de penser que plus il y a de données, meilleure est la statistique. C’est faux, et même grossièrement faux : constituant le paradoxe des big data, il apparaît que la quantité n’est pas gage de qualité (Ouvrir dans un nouvel ongletMeng, 2018), et en voici deux preuves.
Le premier exemple concerne la très récente crise sanitaire. Aux États-Unis, en 2021, trois dispositifs (parmi bien d’autres) ont été conçus pour mesurer la couverture vaccinale des Américains contre le coronavirus (Ouvrir dans un nouvel ongletBradley, 2021). Deux échantillons d’inspiration empirique – le Delphi‑Facebook (DF) et le Census Household Pulse (CHP) – ont été sélectionnés, alors qu’un troisième, conçu par Axios-Ipsos (AI), avait les caractéristiques d’un échantillon probabiliste. L’échantillon DF, organisé en vagues hebdomadaires de 250 000 individus, a cumulé 4,5 millions de répondants entre janvier et mai 2021, pris parmi les utilisateurs actifs de Facebook. Le mode de collecte était (évidemment) un mode de collecte par Internet. L’échantillon CHP, tiré à partir d’un fichier rassemblant des adresses Internet et des numéros de téléphone, cumulait 600 000 réponses obtenues également Online sur la même période. Ces deux échantillons sont issus de tirages aléatoires dans des bases de sondage incomplètes (et même largement incomplète pour DF) et, surtout, sont totalement assimilables à des échantillons de volontaires compte tenu de leurs taux de réponse excessivement faibles (1 % pour DF et 6 à 8 % pour CHP). L’échantillon AI interrogeait 10 000 personnes sur la période. Il a été tiré de manière probabiliste dans une réserve de grande taille, elle-même constituée de manière probabiliste à partir d’une base de sondage d’adresses postales quasi exhaustive. Cette réserve, évoluant au fil du temps, rassemble certes des personnes volontaires pour participer à diverses enquêtes et s’apparente donc en cela à un « Access panel » (Ipsos Knowledge Panel), mais il s’agit en la circonstance d’un dispositif qui maximise les composantes probabilistes et qui est géré et contrôlé comme un échantillon probabiliste, en respectant les bonnes pratiques. Le taux de réponse final AI s’élève à 50 %. L’enquête se déroulait Online mais Ipsos a prêté une tablette à toutes les personnes n’ayant pas accès à Internet. La situation était très favorable pour apprécier la performance de chaque dispositif parce qu’on dispose de la vraie couverture vaccinale : en effet, l’US Center for Disease Control and Prevention est une administration d’État qui compile les statistiques de vaccination reflétant la réalité du terrain. Cela se fait avec un décalage temporel, mais on obtient néanmoins les ‘vraies valeurs’. Tous les échantillons sont repondérés – il s’agit de redressements − afin que certaines structures socio-démographiques soient estimées de manière parfaite. Les résultats sont affligeants : le processus DF surestime en mai 2021 le vrai taux de vaccination (égal à 60 %) de 17 points, le processus CHP le surestime pour sa part de 14 points... et l’échantillon AI propose une estimation qui s’est avérée correcte ! On a vérifié, à partir des données collectées, que l’échantillon empirique hebdomadaire DF (250 000 individus) produit des estimations d’une qualité statistique équivalente à celle d’un échantillon probabiliste de... 10 individus répondants ! Une catastrophe qui s’explique en grande partie par un déséquilibre considérable des deux gros dispositifs selon différents critères, en particulier le niveau d’éducation et l’origine ethnique. En comparant avec les données du recensement, il est apparu clairement que DF et CHP sur-représentent massivement les personnes ayant un niveau d’éducation élevé (poids de l’équivalent du Bac +4 ou plus : 30 % dans la population, 36 % dans AI, 45 % dans DF et 55 % dans CHP) et sous-représentent, dans une moindre mesure, les personnes afro‑américaines et, pour DF, les personnes asiatiques. Tout cela tient à la nature des bases de sondage, du mode de collecte, et d’une stratégie de gestion de la non-réponse très différente selon les enquêtes. Or, il s’avère dans les faits que les personnes à haut diplôme et blanches se font davantage vacciner que les autres catégories de la population américaine. Pressentant le piège, le dispositif CHP a redressé sur l’ethnicité et le niveau d’éducation, limitant ainsi les effets du déséquilibre de l’échantillon interrogé, mais pas DF. Bien que cela n’ait pas été prouvé, on soupçonne également des déséquilibres dommageables portant sur l’opinion politique et sur le partage entre résidence urbaine et résidence rurale. Ce soupçon est fondé, car l’échantillon AI a été redressé en fonction de l’opinion politique (partisanship) et en fonction de la catégorie de commune (metropolitan status), et ce n’est pas le cas des deux autres dispositifs, alors même que l’on sait pertinemment que ces deux variables ont un effet significatif sur la propension à se faire vacciner (par exemple on se fait moins vacciner en milieu rural).
... un précédent tout aussi révélateur
Le second exemple est emprunté à l’histoire (Antoine, 2004 ; Lusinchi, 2012). Dans les années 1930, aux États-Unis, les médias avaient coutume de procéder à des opérations d’enquête dites « vote de paille », consistant à poser des questions par voie postale à des personnes figurant sur des fichiers nominatifs accessibles de diverses natures tels que des abonnés à un magazine, des abonnés au téléphone, des propriétaires de véhicule, ou des listes électorales. Le célèbre Literary Digest a utilisé cette technique en 1936 pour prédire le vainqueur de l’élection présidentielle, qui opposait le démocrate Franklin Roosevelt et le républicain Alfred Landon. Au même moment, trois précurseurs – George Gallup, Elmo Roper et Archibal Crossley – ont utilisé, ce qui était assez nouveau et audacieux, des échantillonnages respectant certains quotas : sans avoir la rigueur des sondages probabilistes, ils s’efforçaient néanmoins de diversifier autant que possible les profils des répondants, et leurs structures selon plusieurs variables étaient « contrôlées ». Chaque sondeur avait conçu son enquête, et les trois échantillons comprenaient chacun quelques milliers ou dizaines de milliers d’individus. En face, le Literary Digest se glorifiait d’avoir collecté deux millions de réponses auprès de volontaires (sans qu’on ne sache précisément la taille exploitée en réalité – mais elle était très importante), qui lui permettaient de prédire une victoire très nette de A. Landon avec 57,4 % des suffrages. Les trois sondeurs annonçaient au contraire la victoire de F. Roosevelt. Le verdict a été sans appel : Roosevelt l’a emporté haut la main avec 61 % des votes. Que s’est-il passé ? Les individus recevant les courriers du Literary Digest étaient plus éduqués et plus fortunés que l’Américain « moyen » : il fallait au moins savoir lire et écrire pour pouvoir répondre, et l’abonnement à des journaux ou la possession de certains biens – téléphone, véhicule entre autres − témoignaient d’une éducation certaine, d’une aisance financière, etc. Ces personnes étaient majoritairement en faveur du parti républicain.
Ces deux exemples illustrent les effets pernicieux d’un échantillonnage insuffisamment contrôlé et insuffisamment corrigé. Ainsi, les big data du Literary digest, de DF et de CHP n’ont paradoxalement pas pesé lourd face aux dispositifs beaucoup moins volumineux mais bien mieux réfléchis de Gallup et d’Axios-Ipsos. Sur le fond, c’est inquiétant parce qu’on peut toujours craindre qu’une variable explicative du phénomène – souvent complexe et protéiforme − que l’on veut mesurer ne soit pas prise en compte ni dans le processus d’échantillonnage, ni lors de l’estimation au travers des redressements. Ce peut être par ignorance, par manque de connaissance des vraies structures, ou pour des raisons de nature culturelle ou juridique. Par exemple, dans les enquêtes menées en France, l’ethnicité et la sensibilité politique − dont on peut penser qu’elles sont corrélées à un certain nombre de comportements – ne sont a priori que rarement prises en considération dans l’établissement des quotas.
L’affaire du Literary Digest a certainement joué un rôle catalyseur dans le développement de la théorie formalisée des sondages probabilistes, qui date de cette époque. Elle a montré en quoi il était sécurisant de produire des estimations issues de sondages dans un cadre mathématique maîtrisé, offrant un minimum de garanties ainsi que des mesures de qualité des estimations produites.
En guise de conclusion
Un échantillon est un objet multidimensionnel complexe qui possède de nombreuses facettes. Il peut être très harmonieux sous certains angles et fort disgracieux sous d’autres si bien que pour l’apprécier pleinement, il faudrait pouvoir l’examiner sous toutes ses faces. Si la taille de l’échantillon répondant est une donnée essentielle pour la qualité d’une enquête, une autre clé du problème réside dans le rôle que l’on confie au hasard. Lorsque la taille de l’échantillon est suffisante, le hasard généré par un algorithme a l’avantage de réduire considérablement le risque de déformation de l’échantillon dans toutes ses dimensions, tandis que celui que l’on attribue à l’homme tout au long du processus de sélection peut s’avérer dévastateur. Confier les échantillonnages empiriques à des structures professionnelles expérimentées permet de réduire les risques de biais. Mais pour éteindre les polémiques touchant à l’échantillon, on peut aussi être tenté de changer la nature du hasard : le hasard des modèles de comportement, traduisant une hypothèse simplificatrice de la réalité, permet de changer de paradigme, offrant un cadre séduisant mais compliqué à comprendre et reportant finalement les risques sur les erreurs de spécification du dit-modèle. Éviter de devoir conditionner les estimations diffusées à cet acte de foi est un argument fort de la Statistique publique pour limiter autant que possible l’utilisation de méthodes empiriques.
Par ailleurs, avec l’expérience des échantillons empiriques on apprend qu’il faut éviter de se fier à la quantité d’information, qui ne protège pas contre le risque de désastre statistique : c’est le paradoxe des big data... dont les journalistes du Literary Digest ont été parmi les premières victimes de l’histoire !
Finalement, si on ne tient pas compte du cas spécifique des très petits échantillons, pour lesquels la technique d’unités-type est la mieux adaptée, en termes d’efficacité statistique et à taille d’échantillon donnée, la méthode probabiliste est toujours préférable à la méthode empirique. Car on sait tirer des échantillons probabilistes respectant des quotas - avant qu’ils ne soient perturbés par la non-réponse : cette méthode magique s’appelle le tirage équilibré (Deville, 2004). Reste aux sondages empiriques l’avantage indéniable de la rapidité de mise en œuvre et de l’économie de moyens.
Paru le :11/12/2023
Il s’agit de bases rassemblant un grand nombre de personnes volontaires pour participer, sous conditions, à des enquêtes portant sur des thèmes variés.
Un principe analogue concerne la correction de la non-réponse dans les enquêtes : un biais survient lorsqu’il subsiste une corrélation entre la variable d’intérêt et la participation à l’enquête une fois que l’on a conditionné par certaines variables explicatives ( jouant un rôle équivalent aux variables de quotas).
Pour en savoir plus
ANTOINE, Jacques, 2004. Histoire des sondages. Éditions Odile Jacob, 20 février 2004. EAN13 : 9782738115874.
ARDILLY, Pascal et LAVALLÉE Pierre, 2017. Les sondages pas à pas. Éditions TECHNIP. ISBN 9782710811794.
ARDILLY, Pascal, 2006. Les techniques de sondage. Éditions TECHNIP. ISBN 978-2-7108-0847-3
ARDILLY, Pascal, CASTELL, Laura et SILLARD Patrick, 2022. Il y a sondage et sondage. In : Blog Insee. [en ligne]. 25 juillet 2022. [Consulté le 10 septembre 2023].
BRADLEY, Valerie C., KURIWAKI, Shiro, ISAKOV, Michael, SEJDINOVIC, Dino, MENG, Xiao-Li et FLAXMAN, Seth, 2021. Ouvrir dans un nouvel ongletUnrepresentative big surveys significantly overestimated US vaccine uptake. Décembre 2021. In: Nature. Volume 600.
BRÜGGEN, Elisabeth, VAN DEN BRAKEL, Jan A. et KROSNICK, Jon, 2016. Ouvrir dans un nouvel ongletEstablishing the accuracy of online panels for survey research. In : site de CBS Statistics Netherland. Discussion Paper. [en ligne]. 11 avril 2016. [Consulté le 10 septembre 2023].
DEVILLE, Jean-Claude et TILLÉ, Yves, 2004. Efficient balanced sampling: The Cube method. In : Biometrika. Décembre 2004. Volume 91, N° 4, pp. 893-912.
DEVILLE, Jean-Claude, 1991. Ouvrir dans un nouvel ongletUne théorie des enquêtes par quotas. In : Techniques d’enquête. [en ligne]. Décembre 1991. Statistiques Canada. Volume 17, N° N2, pp. 177-195. [Consulté le 23 octobre 2023].
FORSTER, Jonathan, 2001. Sample Surveys: Nonprobability Sampling. In : International Encyclopedia of the Social & Behavioral Sciences. Oxford, UK. Elsevier Ltd. Pp. 13467-13470.
LOHR, Sharon L., 2021. Sampling: Designs and Analysis. In : Texts in Statistical Science. 30 novembre 2021. Éditions Chapman & Hall, vol 3. ISBN 978-0367279509.
LUSINCHI, Dominic, 2012. ″President″ Landon and the 1936 Literary Digest Poll: Were Automobile and Telephone Owners to Blame? In : Social Science History. Volume 36, N° 1, pp. 23-54.
MacINNIS, Bo, KROSNICK, Jon A., HO, Annabell S. et CHO, Mu‑Jung, 2018. Ouvrir dans un nouvel ongletThe accuracy of measurements with probability and nonprobability survey samples. In : Public Opinion Quarterly. [en ligne]. 31 octobre 2018. Volume 82, N° N4, pp. 707-744. [Consulté le 10 septembre 2023].
MENG, Xiao-Li, 2018. Ouvrir dans un nouvel ongletStatistical paradises and paradoxes in big data: law of large populations, big data paradox, and the 2016 US presidential election. In : The Annals of Applied Statistics. [en ligne]. Juin 2018. Volume 12, N° 2, pp. 685-726. [Consulté le 23 octobre 2023].
SHIRANI-MEHR, Houshmand, ROTHSCHILD, David, GOEL, Sharad et GELMAN, Andrew, 2018. Ouvrir dans un nouvel ongletDisentangling Bias and Variance in Election Polls. In: Journal of American Statistical Association. [en ligne]. 25 juillet 2018. Volume 13, n° 522, pp. 685-726. [Consulté le 23 octobre 2023].
SMITH, Terence Michael Frederick, 1983. Ouvrir dans un nouvel ongletOn the validity of inferences from non-random samples. In : Journal of the Royal Statistical Society. [en ligne]. Juillet 1983. Volume 146, n° 4, pp. 394-403. [Consulté le 23 octobre 2023].