To compile the samples for household surveys, INSEE relies on a master sample, the construction of which is of defining importance to a statistical institute, as the methodological choices made at this point influence both the quality of the surveys conducted in the next ten years and the way the data collection for these surveys is organised. The master sample, which has long been associated with population censuses, first had to adapt to the methodological changes in the updated census. The availability of tax sources then emerged as a serious alternative. Their use for the Labour Force Survey from 2009 onwards confirmed the potential benefits of INSEE investing in a new master sample, based on the tax files: increased survey accuracy but also efficiency in face-to-face data collection, facilitation of the mixed-mode approach, greater coordination between samples to limit the statistical burden on households, etc. This article summarises the stages that led INSEE to completely update the master sample which will be implemented from 2020.

Official statistics document economic and social facts using many data sources, including long-standing household surveys. In a single operation, these allow a comprehensive overview of the characteristics of individuals and their interactions with the survey theme to be produced. Employment, job security and living conditions, health, income and household wealth, housing and transport are just some of the fields covered by major official statistical surveys. Their contribution to knowledge of social facts is irreplaceable: by using a sample of several thousand households, an inference can be made regarding knowledge about a general population of tens of millions of people. But this is subject to fitting within a strictly scientific frame of reference: the probabilistic sampling theory. This framework combines the principles of random selection of individuals in the survey with a methodology for estimating statistics without bias and with known accuracy, based on this survey. For example, INSEE’s continuous Labour Force Survey, with a sample of 90,000 dwellings, gives an indication of the quarterly unemployment rate to ±0.3 percentage points, with a 95% confidence interval.

This principle of random selection is the only one to guarantee that the analyses of the survey fit with the above theoretical framework. However, it requires the a priori availability of a sampling frame, i.e. a list of households or individuals from the entire population or, failing that, a sub-set, itself derived from a random selection of the general population. Where no sampling frame is available, alternative methods have been developed, such as the quota method. They are very rarely used in the field of official statistics as the estimators they allow to be formed do not spontaneously provide proof of the “right” properties mentioned above. In fact, those estimators are only unbiased and of known accuracy on the generally unverifiable assumption that, subject to the variables on which the quotas are set, the responses given to the questionnaires are random (Ouvrir dans un nouvel ongletDeville, 1991).

The principle of selecting households or individuals randomly in a sampling frame is widely followed in official statistical surveys, regardless of the chosen mode of data collection, whether face-to-face or by phone, or via a self-administered paper or online questionnaire.

Face-to-face interviewing is currently the main method for household surveys managed by INSEE. This method does indeed offer certain advantages, albeit at a cost. For example, it allows a better check to be made of the interviewee’s identity. Above all, it is possible to assess whether the interviewee fully understands the survey context and is interpreting the questions appropriately, and to forestall any reservations they may have by allowing them to talk directly with the interviewer. It also facilitates administration of questioning that is sometimes longer than with other methods of data collection. The face-to-face method is also, of course, more appropriate for reaching people who may not have internet access or who tend not to answer the phone. Other data collection methods such as phone and internet are expanding but face-to-face questioning will most probably remain a significant method in official statistical surveys in the coming years.

Face-to-face collection raises logistical questions about survey access and limitations on interviewers’ travel movements. Indeed, the households liable to be surveyed are split across the entire national territory: if they were selected from the general population for each survey, the interviewers’ travel costs would be prohibitive.

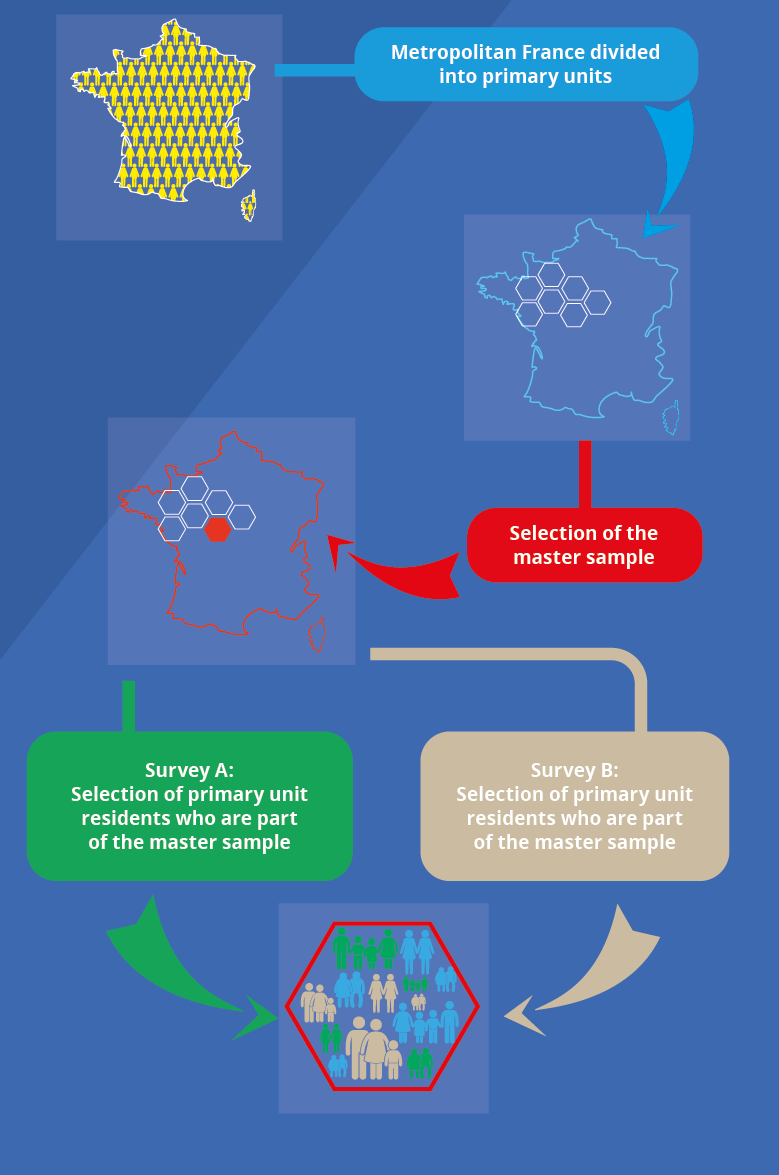
To overcome these inconveniences, there are predefined geographical areas from which the interviewed households are meant to be selected, whatever the survey. To address the principle of random selection, the geographical areas themselves should be selected at random: the national territory will therefore be covered with a geographical distribution of areas, known as primary units. So, the primary units selected define the areas in INSEE’s master sample. When a survey is arranged, the households to be interviewed are randomly selected from those living in the master sample areas (Figure 1).

In order to limit the burden of response, when a household is selected for a survey, we seek to ensure they cannot be selected again subsequently (except as part of a panel survey, of course). But as a result, the master sample areas gradually become depleted and, after about ten years, it is advisable to select a new master sample. It will subsequently be seen that this replacement also becomes necessary for the sake of the initial sample’s effectiveness: over the course of ten years, the population changes, moves and is concentrated in a different way across the territory and there is a gradual deterioration in the representativeness criteria that were initially selected.

Since the sixties, the sampling frame used to form the primary units for INSEE’s surveys had been derived from the population census. This census, called a “general” census up until 1999 because it was exhaustive, saw a change to its methodology from 2004, with the updated or continuous census: the approximately ten-yearly census was replaced with a rotating data collection method over a five-year cycle, with municipalities differentiated by size: below the threshold of 10,000 residents, municipalities are surveyed exhaustively every five years; above this threshold, data collection takes place each year among a sample of 8% of dwellings. This change led to considerable changes being made to the method for constructing the master sample from 2010 onwards (Christine and Faivre, 2009).

Figure 1. The Master Sample Process

In 2017, INSEE had a master sample whose areas, selected in 2010, were gradually becoming depleted and were ultimately likely to become less representative of the territory. A plan was therefore launched, aimed not just at replacing this master sample, but also at rethinking its methodology so as to adapt it to suit new constraints and new requirements. Because in the meantime, the institute had garnered results from a new experiment: the use of tax sources as of 2009 to draw the sample for the LFS, in place and instead of the census (see below).

Its wish to improve productivity and minimise costs meant the institute for official statistics also had to find methodological solutions to optimise the accuracy of its surveys, as this way of thinking was part of an evolving European context. There is now a new general framework, the IESS regulation (Integrated European Social Statistics) for statistical output by EU member states (Cases, 2019). It stipulates, amongst other things, the levels of accuracy to be achieved (or minimum sample sizes for surveys) for certain key indicators, obtained through estimates based on survey data, such as the national or regional unemployment rate or poverty rate, as applicable.

The following sections detail the methodology used for this new master sample for Metropolitan France, in particular with regard to the choice of sampling frame, the definition of the master sample’s primary units and their selection. There is a final section on the work done to replace the LFS sample, which INSEE has decided to select in coordination with the master sample, starting from 2019.

The basic survey sample consists of a list of households or individuals whom the interviewer must be able to interview. In order to do that, they must have the relevant information to make contact with the selected household: residential address, details of type of dwelling, telephone number, email address, etc. In addition to a list of individuals and households, the sampling frame must therefore include variables for contacting them.

It may also usefully contain variables regarding the households’ socio-demographic characteristics. In fact, if variables concerning income, occupation, situation as regards the labour market, etc. are available in the sampling frame, then, inasmuch as they are correlated with the survey’s variables of interest, they allow a sampling plan to be compiled that optimises the accuracy of estimates derived from data collection surveys.

The choice of sampling frame is therefore the result of a trade-off between freshness and coverage in comparison with exhaustiveness and quality of description of the households and the individuals within them. We will see how the scales gradually tipped regarding the choice between the census and the tax sources.

When INSEE used to carry out general censuses, the last of which was in 1999, the sampling frame for INSEE’s household surveys would be constructed at the same time. The primary units were selected at the end of the exhaustive census and the contact details (name, address, etc.) of residents in these areas were kept so they could be interviewed, if applicable. A new census would refresh the sampling frame which, given it aged as people moved house, would be in danger of becoming obsolescent after a ten-year period. The last master sample constructed using this format lasted until 2009 for survey sampling purposes. That year, following ten years of using the frame derived from the final exhaustive census of 1999, the new sampling frame was established, based on the continuous census system.

As before, a list of primary units had been compiled but this time, the people likely to be interviewed in a given year were those in those units of whom a census had actually been taken during the previous annual round of the census. During the 2010s, the sampling for most household surveys was done using this frame. This system benefited from the freshness of the information acquired shortly before the sample was drawn, as part of the latest annual round of the census.

But there was one drawback that emerged over time, related to the method for selecting municipalities in the census. For municipalities with fewer than 10,000 residents, the annual census is based on a programme consisting of a rotating sample of municipalities, designed to cover all of them over a 5-year period. This annual sample of municipalities is the result of balanced sampling based on 1999 census data. Having been in use for around twenty years, demographic and social changes meant this sample no longer reflected the original balanced situation. This flaw, the scale of which depends on the variable of interest, is generally reflected in an increase in the mean square error by a ratio of 2 to 20, compared with a sample drawn from an exhaustive sampling frame (Favre-Martinoz, 2015).

As the end of the 2010s approached, the 2009 master sample therefore needed to be replaced and the initial methodological work began in 2017.

INSEE already had about ten years of sound experience in using tax sources for drawing survey samples. In fact, the 2009 LFS sample had been drawn using the housing tax records (Loonis, 2009).

These data offer a virtually exhaustive view of the households living in France and of their dwellings, which are also subject to property tax and land registry monitoring. They are therefore very precisely located, by land registry plot, meaning accuracy to within a few metres of the related geographical coordinates. This therefore allows the formation of geographical proximity-based clusters for the LFS. It was this specific feature that justified basing the LFS sample on tax sources in 2009.

Since then, other household surveys have used sampling based on tax sources, notably surveys on household wealth. The use of these sources is becoming widespread and, in 2016, INSEE set up an annual production derived from the statistical alignment of tax sources. The files created in this way – called Fidéli, Fichiers Démographiques sur les Logements et les Individus, (Demographic Files on Dwellings and Individuals) - constitute a high-quality information base. In comparison with the raw data derived from tax management, the Fidéli source pays special attention to the issues of double counting and field coverage, notably by ensuring maximum comparability between the concepts it uses and those of the census. For example, communities are identified as part of the Fidéli process whereas, strictly speaking, they are not located in the raw tax data (Ouvrir dans un nouvel ongletMerly-Alpa and Sillard, 2019).

Fidéli also includes many interesting variables to use for sampling purposes and when gathering survey data. These include contact variables (dwelling address, email addresses and phone numbers), description variables for dwellings and household composition, and income variables. Such variables may be used ex ante for balancing or stratification purposes, and ex post for making adjustments. The main differences between Fidéli and the census relate to the variables on occupation and social category, educational qualifications and income, the last of which only features in Fidéli, whereas the others only feature in the census. Incomes are known to be correlated with many socio-demographic variables, therefore their presence in the sampling frame constitutes a significant advance. On balance, therefore, Fidéli appears to constitute a strong candidate for serving as the main sampling frame, instead of the census. That was the choice made for constructing the master sample and LFS sample in 2020.

INSEE employs a network of around 850 interviewers who can reasonably carry out data collection waves for household surveys, distributed across around 500 primary units. Interviewers are assigned a data collection area, generally formed around one of the master sample’s primary units. The extent of these areas must therefore be appropriate so they can be covered by an interviewer. Although different configurations were assessed, it seemed simpler, including in terms of fieldwork organisation, to construct primary units in the form of groups of adjacent municipalities.

INSEE interviews about 500,000 households every year. In order to limit the data collection burden on households, the primary units are also designed to avoid re-interviewing a household staying in the same dwelling over a five-year period.

Given these various constraints, primary units for household survey samples consist of a minimum of 2,500 dwellings, thus ensuring a reserve in the event of more extensive use.

Lastly, to facilitate management of the interviewers and their data collection area, each primary unit is fully contained within one department of France. This also allows the underlying problem of optimisation to be devolved to this level.

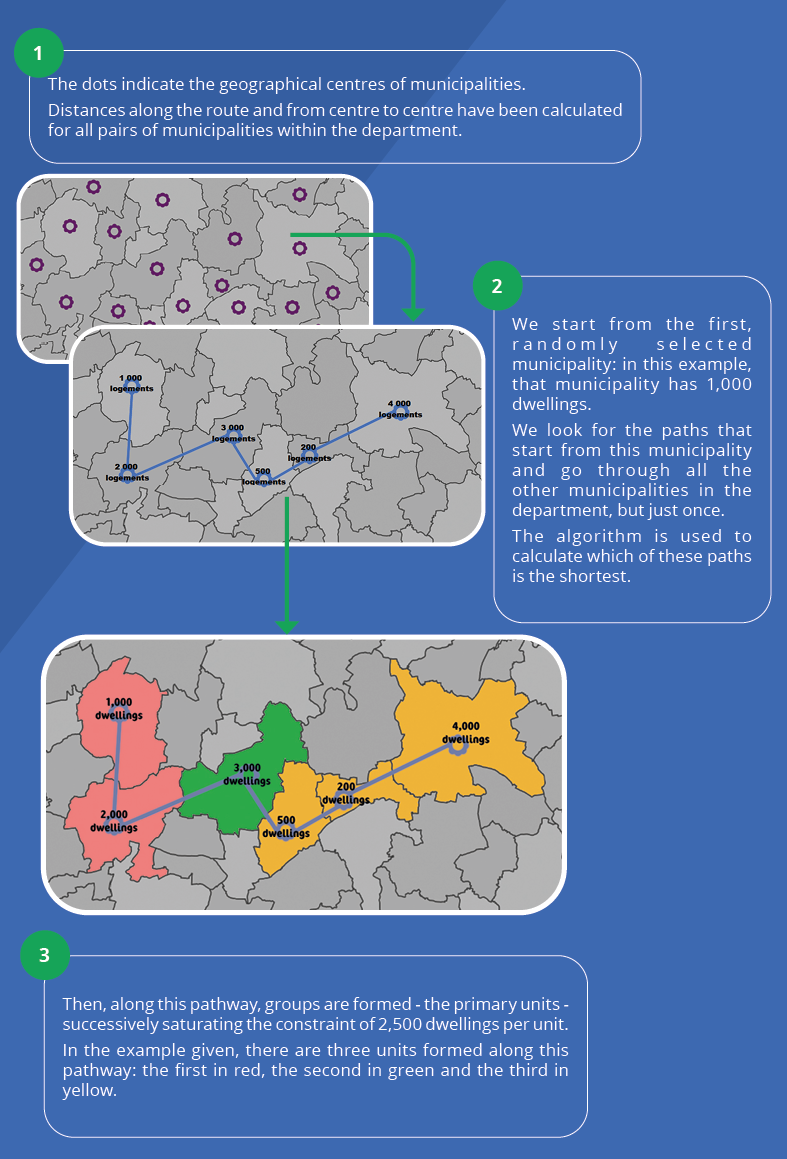
The problem was worded as follows: for each department, you have to cover the barycentres of the municipalities within the department, setting off from one of them, selected at random, then taking the shortest path and returning to your starting point, only passing through each municipality once. This closed path, which is dependent only on the starting municipality, is calculated using an algorithm for solving the Travelling Salesman Problem (Applegate et alii, 2006). The calculation can be repeated as many times as there are municipalities within the department.

Then, for each path calculated, the related primary units are determined, travelling throughout the municipalities along the way and gradually saturating the constraint on the number of dwellings in the primary unit, which must be greater than 2,500. When a unit of more than 2,500 dwellings is formed, the construction of a new unit is launched by moving to the next municipality on the path (Figure 2). Each path therefore corresponds to a division of the department into primary units, in accordance with the constraint on the number of dwellings.

The geographical extent of a primary unit is then defined by the average distance along the route between the centre of the main municipality and the centre of the other municipalities within the unit, weighted by the number of dwellings in these other municipalities besides the main one. At departmental level, the average geographical extent of the primary units covering the department determines an objective value that characterises the resulting division and path followed.

The geographical extent related to a departmental division is also understood to mean the average distance covered in accessing the dwellings from the centre of the primary units so formed. This matter directly concerns the interviewers doing the fieldwork: the geographical extent of the area they have to cover to collect data will have a direct impact on their travel costs and time, so ought to be minimised.

Finally, out of all the paths calculated, the one with the smallest objective value is chosen: this path corresponds to the average geographical extent of the primary units, the smallest of the different divisions formed for the department concerned. On average, through implementing the above-mentioned optimisation plan, the geographical extent of primary units in Metropolitan France has decreased by 25% compared with the 2010 master sample.

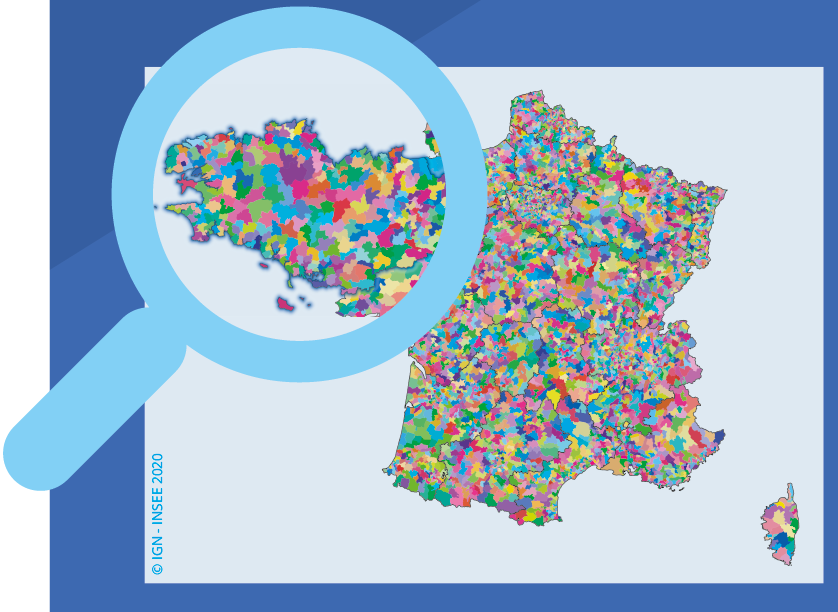
However, the method does not allow consideration of certain local specific characteristics related to the presence of a national border, saturation of certain networks or the closing of certain roads, which may alter assessment of the geographical extent. The map of primary units has therefore been amended on occasion, following assessment by INSEE’s regional offices. The work has ultimately led to the division of Metropolitan France into 5,128 primary units (Figure 3).

Figure 2. How to Construct Primary Units Along a Given Pathway

Figure 3. Whith the New Master Sample, Metropolitan France Has 5,128 Primary Units

One of the main issues for INSEE is controlling the accuracy of its surveys. As we have seen, in practice, there are two non-simultaneous steps to the sampling process for these surveys. The first, known as “stage one sampling”, consists of selecting the primary units of the master sample. This first stage takes place once every ten years. Then, for each survey, a sample is drawn of dozens of the resident households in each primary unit of this master sample through a “stage two sampling” process and these selected households will then actually be interviewed for that survey. The survey’s accuracy is the result of these two sampling stages: the selection of the primary units and of the households resident in these primary units.

The two stages of sampling are independent of one another so the variance of an estimator, for example of a mean or total based on the survey sample polled, breaks down into two separate terms that add up.

More precisely, it has been shown (Ouvrir dans un nouvel ongletTillé, 2019) that the variance of a mean or total estimator breaks down into two terms: a variance term known as “first stage”, related to the variance in the variable totals observed within each primary unit, plus a second term, known as “second stage”, related to the sum of the intra-primary unit variances. First stage variance is independent of second stage variance and the latter is also essentially independent of first stage variance, apart from through the presence, in its expression, of a scale factor inversely proportionate to the first stage sampling rate: if the number of primary units selected is reduced, all else being equal, second stage variance increases proportionately. But this interaction is modest and controllable, so variance optimisation can therefore be separated out, which proves to be very practical as first and second stage sampling are not done simultaneously.

Optimisation of first stage sampling can therefore be summarised as forming an optimal sampling plan, i.e. one that minimises the first stage variance associated with the 500 or so primary units to be selected from the total of 5,128 in Metropolitan France.

To put together this plan, we have the variables from the sampling frame (Fidéli) and also all the variables taken from INSEE’s social statistics output by individual municipality, which can be calculated for groups of municipalities combined together. This is actually one of the major benefits of constructing primary units in the form of groups of municipalities, whereas other solutions could have been considered but would have made producing a set of related statistics more complex.

So, in practice, we have a large amount of a priori known information about the primary units: number of people by gender and age derived from the census, socio-professional category, qualifications and educational level, work activity, household composition, wages, income, business profits, numbers subject to wealth tax, housing characteristics, regions to which they belong, etc.

And knowledge of these statistics is a decisive factor in first stage variance. In fact, first stage sampling is, by its nature, unaffected by any potential non-response, since any primary unit in the master sample will be covered by data collection in all circumstances. Consequently, the most worthwhile sampling plans are those that are balanced in terms of certain variables: in these plans, the samples systematically verify the equality of estimators of means with their true values in the population as a whole, as these true values are also known, for example through the census.

Sampling algorithms allow only the selection of balanced plans, or plans that approximate strict balancing, if that is not entirely possible. That is the case with the Cube Method (Ouvrir dans un nouvel ongletDeville and Tillé, 2004). Balancing is particularly worthwhile when there is a statistical correlation between one of the survey’s variables of interest and the balancing variables: if the latter help explain the variables of interest, in the sense of a linear regression, then it can be seen that the variance in estimators derived from sampling is in the order of the level of variability in the regression residuals rather than in the variable of interest. It is therefore advisable to choose balancing variables that best explain the surveys’ future variables of interest. However, in designing the plan, it is advisable to limit the interplay of balancing variables which, de facto, limit the field of randomness in the selection of primary units.

Now the number of primary units is relatively low (5,128), and likewise the number of units selected (about 500). Consequently, the highly decisive nature of the balancing constraints, mainly related to their number, is reached quite quickly. For example, introducing too many balancing variables would lead to no longer being able to comply with the principle of a set size of master sample in terms of the number of primary units.

A Principal Component Analysis (PCA) has led to a reduction in balancing variables on the first 15 axes, representing 99% of the inertia of all available variables. This representation of almost all the information on the population through the sample obtained is done, however, at the expense of the perfect balancing of the sample on a limited number of variables. That is why these axes are supplemented with certain key variables, such as population or those for ensuring a set number of master sample units in each region. Lastly, the plan is balanced regionally, with a national landing phase to ease the constraints that cannot be met at a regional level (Ouvrir dans un nouvel ongletChauvet, 2009).

Selecting the plan, and therefore the variables chosen for balancing purposes, is based on empirical optimisation of the coefficient of variation of the variables of interest. Technically, this coefficient of variation can be approximated by using a Monte Carlo method to carry out numerous simulations of the chosen sampling plan, with the empirical mean and variance for the estimates produced through each simulation converging on the true value of the estimators. These estimators are calculated at national and regional level, due to the constraints in the IESS regulation regarding these two geographical levels. The chosen sample sizes and first stage sampling plan are therefore designed to comply with European constraints.

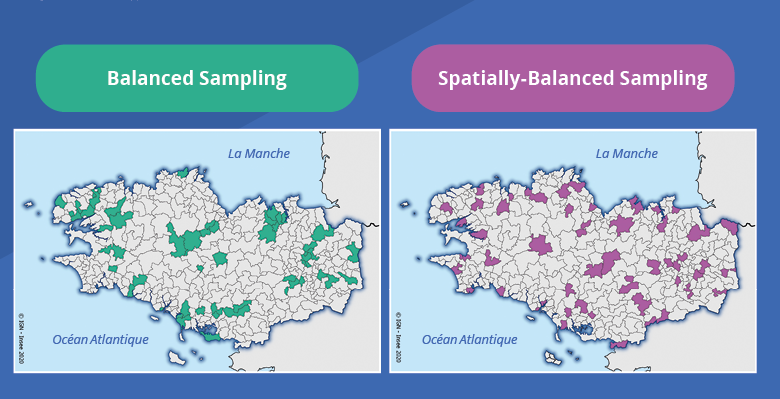
The balancing method ultimately selected is a variant of the Cube algorithm, known as “doubly balanced sampling”, adapted to suit situations in which the variables of interest are spatially correlated, which is the case with most socio-economic variables. In fact, in this type of situation, all else being equal, two units that are close together will provide somewhat less statistical information than two units that are further apart (Loonis and De Bellefon, 2018). It will therefore be worth selecting units modulo a slight repulsive force between units close to one another, resulting in a sample with better spatial distribution (Figure 4). That is the purpose of the spatial balancing algorithm developed by (Ouvrir dans un nouvel ongletGrafström and Tillé, 2013), and applied in this case. Simulations show that, for spatially correlated variables that do not contribute to balancing, such as the number of managers or unemployed people, the gains made in spatial balancing can represent up to 20% in terms of mean square error of estimates, compared with single balancing (Ouvrir dans un nouvel ongletFavre-Martinoz and Merly-Alpa, 2016).

The master sample sets the geographical areas in which the data for most of INSEE’s household surveys are collected. However, for reasons primarily related to survey protocol, data collection for the LFS is carried out in separate areas from those of the master sample. It seemed wise to reconcile these data collection areas to facilitate interviewer activity. That is what has been done for the first time in this exercise.

Figure 4. Spacial Balanced Effect on Primary Unit Selection

The LFS stands out from household surveys due to its very short data collection period (three weeks in the quarter), forcing the interviewer doing the fieldwork to cover the area rapidly. That is one of the reasons for selecting its sample by clusters of dwellings that are geographically close to one another.

In 2009, the LFS sample was selected independently of the master sample. The course of action taken for this replacement (Loonis, 2009) involved reliance on tax sources to form the data collection sectors, each comprised of six clusters, each containing about 20 almost adjacent dwellings. Metropolitan France is divided into 232,000 LFS sectors, comprised of 1.4 million clusters, grouping together 28.3 million main residences. A sector sample was drawn. All dwellings in a sampled cluster were interviewed over six consecutive quarters (for more details, see Box 1), and were then replaced with dwellings from another cluster in the same sector. The LFS sample thus has a nine-year lifespan.

In 2019, the wish to optimise the data collection activity of INSEE’s interviewers led to consideration being given to coordinating the samples for the LFS and for other household surveys.

An initial idea could have been to select LFS sectors within the primary units of the master sample. But firstly, this would have led to the rapid exhaustion of certain primary units that were too small; and secondly, the level of accuracy of estimators derived from the LFS would have been below expectations, particularly in light of the IESS regulations. This solution was therefore very quickly dropped in favour of a solution consisting of defining neighbourhoods of selected primary units, within which the LFS sectors will be sampled. These neighbouring areas constitute coordination units.

A detailed analysis of the different options was carried out, notably in regard to the size and number of primary units constituting the coordination units and based on considerations related to the accuracy of the two types of survey. This led to the decision to set a minimum coordination unit size of 10,000 dwellings / main residences, compared with a minimum primary unit size of 2,500 dwellings.

In terms of the selection mechanism, the coordination units appear to be indirectly selected, following sampling of the primary units in the master sample. Several primary units can be the source of a single coordination unit. This therefore takes us into the context of indirect sampling (Ouvrir dans un nouvel ongletDeville and Lavallée, 2006) which requires a weight share procedure.

Once the coordination units have been defined, these contain the LFS sectors that, like the primary units of the master sample, are subject to spatially balanced sampling. The sectors are independently selected from one region to another (regional stratification), which allows appropriate adjustment to regional sample sizes according to the constraints of the IESS European regulation.

As with the master sample, Monte Carlo simulations help clarify the parametrisation of the sampling plan, through analysis of details obtained on proxies of the variables of interest in the LFS, based on variables in the sampling frame. That is the case, for example, with the working activity variable, for which a proxy, based on the tax data, is the non-zero earnings dummy.

The overall plan requires optimisation, since the two samples are strongly connected, due to introducing coordination: a variation in the number of primary units chosen has an effect on the accuracy of household surveys and of the LFS. The number of sectors also affects the accuracy of the LFS. So there are several possible mechanisms for example for improving the accuracy of the LFS: the number of primary units selected, the size of the coordination units and the number of sectors. Simulations are done to assess the impact of the different parameters in terms of accuracy. These results are compared with the levels of accuracy that must be achieved in light of the IESS framework regulation.

The ultimate result of all the measures taken to improve accuracy is a spectacular improvement by a factor of 5 to 6 in the level of first stage accuracy for the new master sample, compared with the one based on the annual census surveys.

By redoing the simultaneous sampling for the two samples, it is possible to make estimates of accuracy converging on the true, known values for variables in the sampling frame. Tens of millions of samples of primary units and LFS sectors were selected, in numerous different configurations, to arrive at a choice regarding parametrisation. This related to the configuration of geographical areas, in particular as regards the lower threshold for the number of dwellings per primary unit and per coordination unit, the balancing variables and sample sizes, i.e. the number of areas selected within the chosen samples.

The final target parameters were the numbers of units selected per region: these allowed for refinement of the scenarios presented to INSEE’s Executive Committee and the regional offices responsible for managing the interviewers. They were initially proportionate to the size of region (in terms of the number of main residences), then were subsequently boosted in small regions to the detriment of larger ones, so as to avoid excessive concentration of LFS sectors in the vicinity of too limited a number of primary units. Sampling simulations were able to verify that the expected accuracy regarding the main variables in the LFS appeared compatible with the distribution requirements. The final validation procedure resulted in a sample of 541 primary units, from which a selection was made of 524 coordination units and lastly, 2,944 sectors for the LFS (note).

Of course, total variance is also dependent on the second stage which is itself dependent on sample size (number of households sampled in each primary unit). As the distribution of variance between the first and second stage is so varied, it is advisable not to reduce the number of primary units too much on the basis that first stage accuracy would be very favourable. Necessary caution led to the selection of a slightly lower number of units compared with the previous sample, dropping from 567 to 541.

In many identical sectors selected, only modest spontaneous improvements in LFS accuracy are expected from the methodological changes, as the previous sample had already been constructed from the tax records (Loonis, 2009). However, the new ability, made possible through the availability of the Fidéli source, to balance sector sampling on proxies of unemployment variables, for example, has constituted a substantial improvement. On the other hand, coordinating the two samples generates extra variance in the LFS. Bearing in mind the expected gains in regard to the first stage for household surveys, it was possible to adjust the number of primary units selected per region in such a way as to ensure a level of regional accuracy in the LFS that is compatible with the IESS regulation constraints, despite the spontaneous loss of accuracy due to coordination. A slight reduction in the number of LFS sectors was also possible as an assessment of survey accuracy indicates that the marginal gain associated with the primary units is markedly more favourable than the gain associated with the sectors, owing to the cluster effect that is characteristic of the latter.

Updating the samples for household surveys and the LFS is a strategic project for INSEE. It addresses the wish to be able to conduct surveys based on a solid, proven methodology that is appropriate for the face-to-face data collection method.

Alternative methods (internet, telephone and paper) are growing, due to their flexibility and lower cost and because they are better for reaching certain household categories: strictly speaking, they do not require a master sample. Moreover, INSEE is actively strengthening its ability to run mixed-mode surveys (Cotton and Dubois, 2019; Koumarianos and Sigaud, 2019). But in a large country like France, the principle of a master sample remains most appropriate for face-to-face data collection, whether as the sole collection mode or as a component in a mixed-mode survey.

The project has also been demanding. Carried out in agile mode, with strong interaction between the designers and developers, it has involved three experts from the Methodology Directorate working on it full-time for 18 months. The deployment of interviewers in the new areas was assessed and determined by the regional offices and the Demographic and Social Statistics Directorate, in consultation with the trade union organisations. Besides the methodological and organisational aspects, a specific application was developed: NAUTILE standardises and increases the security of drawing samples from the master sample and marks the dwellings selected for a survey. This application is compatible with the active metadata management tools already in use. Through its samples, it will feed into the applications for managing surveys, calculating interviewer load and handling administration of contacts for the households for the next ten years.